Strassen algoritması iki matrisin çarpımını daha az çarpma işlemi yaparak, zaman karmaşasını azaltmak için tasarlanmış bir algoritmadır. Matris çarpımları özellikle Bilgisayar Grafikleri'nde (Computer Graphics) önemli bir yer tutar çünkü objeleri döndürmek, yeniden boyutlandırmak, pozisyonlarını değiştirmek gibi işlemler matrisler ile yapılır.

Strassen algoritmasına geçmeden önce iteratif (naive method) ve rekürsif (divide and conquer) olmak üzere iki algoritma ile matris çarpımını nasıl bulabiliriz bir bakalım.
Naif Yöntem (Naive Method)
public static float[][] naiveMult(float[][] M1, float[][] M2)
{
// Matris çarpımının tutulacağı matris.
float[][] mult = new float[M1.length][M2[0].length];
for(int i = 0; i < M1.length; i++)
{
for(int j = 0; j < M2[0].length; j++)
{
for(int k = 0; k < M2.length; k++)
{
// M1'in i. satırı ve M2'nin j. sütununun
// çarpımından elde edilen toplam.
mult[i][j] += M1[i][k] * M2[k][j];
}
}
}
return mult;
}
Öncelikle elimizde n x n boyutlarında iki matrisin olduğunu varsayalım. Algoritma, 3 döngüden oluşmaktadır ve her bir döngü n kadar dönmektedir. Bu da algoritmanın karmaşasının O(n3) olduğunu gösterir.
Böl ve Fethet (Divide and Conquer)
Böl ve fethet algoritmaları bir problemi benzer alt problemlere indirgeyerek problemi kolayca çözülebilecek temel bir adıma götürür. Bu sayede rekürsif olarak problemi çözebiliriz. Peki iki matrisin çarpımını rekürsif olarak nasıl ifade edebiliriz? Bunu iki adımla şöyle tanımlayabiliriz:
- A ve B matrislerini N/2 x N/2 boyutlarında 4 alt matrise böl.
- Rekürsif olarak ae + bg, af + bh, ce + dg ve cf + dh -yi hesapla.
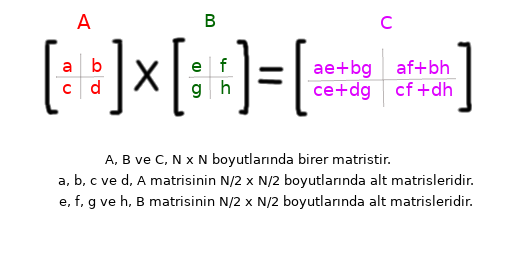
Yukarıdaki şekildende görülebileceği gibi A ve B matrislerinin her bir alt matrisinin çarpımları bize C matrisini verir. Bu aslında iki matrisi çarpmaya benzer fakat burada dikkat edilecek husus a, b, c, d, e, f, g ve h -nin birer birer matris olduğudur. Bunu kağıt kalemle deneyip doğrulamanız daha iyi anlamanızı sağlayacaktır. Şimdi bu algoritmayı koda nasıl dökeriz bir bakalım.
public static float[][] divideAndConquerMult(float[][] m1, float[][] m2)
{
// Bu yöntemi uygulayabilmek için matrislerin 2^n x 2^n boyutlarında olması
// gerekli. Eğer değillerse matrisleri en küçük 2^n x 2^n boyutunda birer
// matrise dönüştürmemiz gerekli. Bunu dolgulama (padding) ile kolayca
// yapabiliriz.
// 2x3-lük bir matris 0 ile dolgulanarak 4x4 lük bir matris haline
// getirilmiştir.
//
// [ 2 3 4 0 ]
// [ 2 3 4 ] ===> [ 1 5 7 0 ]
// [ 1 5 7 ] ===> [ 0 0 0 0 ]
// [ 0 0 0 0 ]
//
// Matrisin sıfırlarla doldurulması çarpma işleminin sonucu etkilememektedir.
// getPadSize, dolgulama sonrası matrisin boyutunun ne olacağını döndürür.
int n = getPadSize(m1, m2);
float[][] M1 = addPadding(m1, n);
float[][] M2 = addPadding(m2, n);
float[][] R = new float[n][n];
// Temel adım: Eğer n == 1 ise 1x1-lik iki matrisi çarparız.
if(n == 1)
{
R[0][0] = M1[0][0] * M2[0][0];
return R;
}
int nd2 = n / 2;
float[][] A = new float[nd2][nd2];
float[][] B = new float[nd2][nd2];
float[][] C = new float[nd2][nd2];
float[][] D = new float[nd2][nd2];
float[][] E = new float[nd2][nd2];
float[][] F = new float[nd2][nd2];
float[][] G = new float[nd2][nd2];
float[][] H = new float[nd2][nd2];
// İlk matrisi alt matrislere böl.
split(M1, A, 0, 0);
split(M1, B, 0, nd2);
split(M1, C, nd2, 0);
split(M1, D, nd2, nd2);
// İkinci matrisi alt matrislere böl.
split(M2, E, 0, 0);
split(M2, F, 0, nd2);
split(M2, G, nd2, 0);
split(M2, H, nd2, nd2);
/*
R11 = AE + BG
R12 = AF + BH
R21 = CE + DG
R22 = CF + DH
*/
float[][] R11 = add(divideAndConquerMult(A, E), divideAndConquerMult(B, G));
float[][] R12 = add(divideAndConquerMult(A, F), divideAndConquerMult(B, H));
float[][] R21 = add(divideAndConquerMult(C, E), divideAndConquerMult(D, G));
float[][] R22 = add(divideAndConquerMult(C, F), divideAndConquerMult(D, H));
// Hesaplanan alt matrisleri birleştir.
merge(R, R11, 0, 0);
merge(R, R12, 0, nd2);
merge(R, R21, nd2, 0);
merge(R, R22, nd2, nd2);
// En sonunda dolguyu kaldırmamız gerekli.
R = removePadding(R, m1.length, m2[0].length);
return R;
}
Yukarıdaki algoritmada her bir alt matrisin hesaplanması için 8 çarpma ve 4 toplama işlemi yapılıyor. İki matrisi O(n2) zamanda toplayabiliriz. Bu durumda karmaşıklığı şöyle ifade edebiliriz:
Master Teoremine göre yukarıdaki karmaşıklık O(n3)'tür. Bu da bize en baştaki iteratif yöntemden daha iyisini yapamadığımızı gösterir.
Strassen'in Algoritması
Yukaridaki böl ve fethet algoritmasında her bir alt matrisi hesaplayabilmek için 8 rekürsif çağrı yapıyoruz. Strassen'in fikri bu rekürsif çağrıları 7'ye düşürmekti. Strassen algoritmasında alt matrislerin nasıl hesaplandığını aşağıdaki şekilden inceyebilirsiniz.
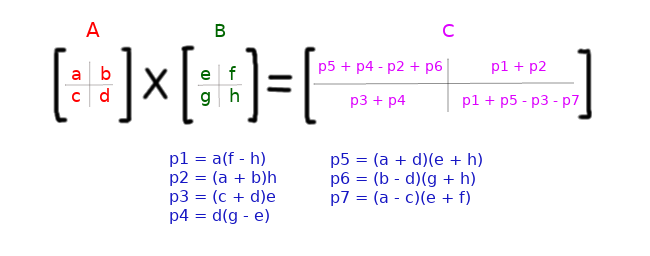
Yukarıdaki şekildende anlaşılabileceği gibi p1, p2, p3, p4, p5, p6 ve p7 birer N/2 x N/2 -lik matrislerdir. Burada her alt matrisi hesaplarken 7 çarpma işlemi yapıyoruz. Bu da daha az rekürsif çağrı yapacağımız anlamına gelir. Toplama ve çıkarma işlemleri ise yine O(n2) zamanda yapılabilir. Elimizdeki bu bilgilere dayanarak Strassen algoritmasının zaman karmaşasını şu şekilde yazabiliriz:
Master Teoremine göre yukarıdaki karmaşıklık O(nlog27)'dir. Bu da yaklaşık olarak O(n2.8)'dir.
public static float[][] strassenMult(float[][] m1, float[][] m2)
{
// Böl ve fethet algoritmasında yaptığımız gibi burada da matris
// boyutları 2^n x 2^n değilse dolgulama yapmamız gerekli.
int n = getPadSize(m1, m2);
float[][] M1 = addPadding(m1, n);
float[][] M2 = addPadding(m2, n);
float[][] R = new float[n][n];
if(n == 1)
{
R[0][0] = M1[0][0] * M2[0][0];
return R;
}
int nd2 = n / 2;
float[][] A = new float[nd2][nd2];
float[][] B = new float[nd2][nd2];
float[][] C = new float[nd2][nd2];
float[][] D = new float[nd2][nd2];
float[][] E = new float[nd2][nd2];
float[][] F = new float[nd2][nd2];
float[][] G = new float[nd2][nd2];
float[][] H = new float[nd2][nd2];
// İlk matrisi alt matrislere böl.
split(M1, A, 0, 0);
split(M1, B, 0, nd2);
split(M1, C, nd2, 0);
split(M1, D, nd2, nd2);
// İkinci matrisi alt matrislere böl.
split(M2, E, 0, 0);
split(M2, F, 0, nd2);
split(M2, G, nd2, 0);
split(M2, H, nd2, nd2);
/* Strassen'in formülü
P1 = A * (F - H)
P2 = (A + B) * H
P3 = (C + D) * E
P4 = D * (G - E)
P5 = (A + D) * (E + H)
P6 = (B - D) * (G + H)
P7 = (A - C) * (E + F)
*/
float[][] P1 = strassenMult(A, sub(F, H));
float[][] P2 = strassenMult(add(A, B), H);
float[][] P3 = strassenMult(add(C, D), E);
float[][] P4 = strassenMult(D, sub(G, E));
float[][] P5 = strassenMult(add(A, D), add(E, H));
float[][] P6 = strassenMult(sub(B, D), add(G, H));
float[][] P7 = strassenMult(sub(A, C), add(E, F));
/* Strassen'in formülü
R11 = P5 + P4 - P2 + P6
R12 = P1 + P2
R21 = P3 + P4
R22 = P1 + P5 - P3 - P7
*/
float[][] R11 = add(sub(add(P5, P4), P2), P6);
float[][] R12 = add(P1, P2);
float[][] R21 = add(P3, P4);
float[][] R22 = sub(sub(add(P1, P5), P3), P7);
// Alt matrisleri birleştir.
merge(R, R11, 0, 0);
merge(R, R12, 0, nd2);
merge(R, R21, nd2, 0);
merge(R, R22, nd2, nd2);
R = removePadding(R, m1.length, m2[0].length);
return R;
}
Gördüğünüz gibi Strassen algoritması, böl ve fethet algoritmasıyla aynı. Değişen tek şey alt matrislerin nasıl hesaplandığı. Daha önce 8 çarpma yapıyorduk, Strassen algoritmasında ise 7 çarpma yapıyoruz. Bu sayede daha az rekürsif çağrı yapmış oluyoruz. Bu da zaman karmaşasını O(n3)'ten O(n2.8)'e düşürüyor.
Sonuç
Sonuç olarak Strassen algoritmasının zaman karmaşıklığı diğer algoritmalara göre daha iyidir fakat pratikte işler pekte öyle değildir. Bunun bazı sebepleri şöyledir:
- Strassen algoritmasında yapılan sabit işlemler naive metotda yapılana göre daha fazladır.
- Her rekürsif çağrıda alt matrislerin oluşturulması zaman ve bellek açısından ekstra bir yüktür.